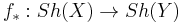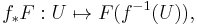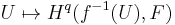Direct image functor
In mathematics, in the field of sheaf theory and especially in algebraic geometry, the direct image functor generalizes the notion of a section of a sheaf to the relative case.
Contents[hide] |
Definition
| Image functors for sheaves |
|---|
| direct image f∗ |
| inverse image f∗ |
| direct image with compact support f! |
| exceptional inverse image Rf! |
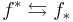 |
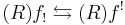 |
Let f: X → Y be a continuous mapping of topological spaces, and Sh(–) the category of sheaves of abelian groups on a topological space. The direct image functor
sends a sheaf F on X to its direct image presheaf
which turns out be a sheaf on Y. This assignment is functorial, i.e. a morphism of sheaves φ: F → G on X gives rise to a morphism of sheaves f∗(φ): f∗(F) → f∗(G) on Y.
Example
If Y is a point, then the direct image equals the global sections functor. Let f: X → Y be a continuous map of topological spaces or a morphism of schemes. Then the exceptional inverse image is a functor Rf!: D(Y) → D(X).
Variants
A similar definition applies to sheaves on topoi, such as etale sheaves. Instead of the above preimage f−1(U) the fiber product of U and X over Y is used.
Higher direct images
The direct image functor is left exact, but usually not right exact. Hence one can consider the right derived functors of the direct image. They are called higher direct images and denoted Rq f∗.
One can show that there is a similar expression as above for higher direct images: for a sheaf F on X, Rq f∗(F) is the sheaf associated to the presheaves
Properties
- The direct image functor is right adjoint to the inverse image functor, which means that for any continuous
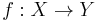 and sheaves
and sheaves 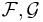 respectively on X, Y, there is a natural isomorphism:
respectively on X, Y, there is a natural isomorphism:
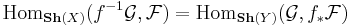 .
.
- If f is the inclusion of a closed subspace X ⊂ Y then f∗ is exact. Actually, in this case f∗ is an equivalence between sheaves on X and sheaves on Y supported on X.
References
- Iversen, Birger (1986), Cohomology of sheaves, Universitext, Berlin, New York: Springer-Verlag, ISBN 978-3-540-16389-3, MR842190, esp. section II.4
This article incorporates material from Direct image (functor) on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.